- 118金宝搏
-
pingwen平文—高品质仓配服务商全温区金博宝188电子游艺app网址 物流一体化解决方案
平文智慧云仓-13年专注第三方电商云仓代发货服务,提供:仓储+分拣+打包+二次加工等综合性仓储物流方案;包括常温仓储,恒温恒湿仓储,冷链仓储服务,电商云仓一件代发,电商仓储物流......
 20万㎡高标仓库全温区电商一件代发云仓
20万㎡高标仓库全温区电商一件代发云仓 定制化仓配方案1V1服务
定制化仓配方案1V1服务 数字化供应链管理智慧云仓+智慧物流
数字化供应链管理智慧云仓+智慧物流 10年大促经验日500万订单处理量
10年大促经验日500万订单处理量
平文智慧云仓-13年专注第三方电商云仓代发货服务,提供:仓储+分拣+打包+二次加工等综合性仓储物流方案;包括常温仓储,恒温恒湿仓储,冷链仓储服务,电商云仓一件代发,电商仓储物流......
 20万㎡高标仓库全温区电商一件代发云仓
20万㎡高标仓库全温区电商一件代发云仓 定制化仓配方案1V1服务
定制化仓配方案1V1服务 数字化供应链管理智慧云仓+智慧物流
数字化供应链管理智慧云仓+智慧物流 10年大促经验日500万订单处理量
10年大促经验日500万订单处理量
平文是’AAAA'级物流企业-自有车队,车辆达800+辆,包括厢式车,平板车,冷藏车等多种车辆,满足不同产品的运输需求,所有车辆无毒、无异味、清洁平整,
与三通一达,顺丰等快递达成深度战略合作,当天下午四点前订单,可当天发出,降低快递/物流成本,提高货物运输效率!

13年仓储代发货经验,涵盖常温仓,恒温恒湿仓,冷藏冷冻仓,温度按需定制,灵活选择仓储面积,提供人性化的淡旺季灵活用仓服务,
布局全国金博宝188电子游艺app网址 服务网络,在华北,华东,华中,西南区域13座城市建有仓储配送基地.

20万㎡仓库均配有完善的硬件设备:输送线,液压车,分拣平台,包装平台等,提供仓储+质检+包装+二次加工+退换货等一站式仓储配送服务体系,
公司自主研发:WMS+TMS+OMS等全方位智能化信息系统,打造订单及时处理,货物信息可追踪等智慧云仓,智慧物流体系.
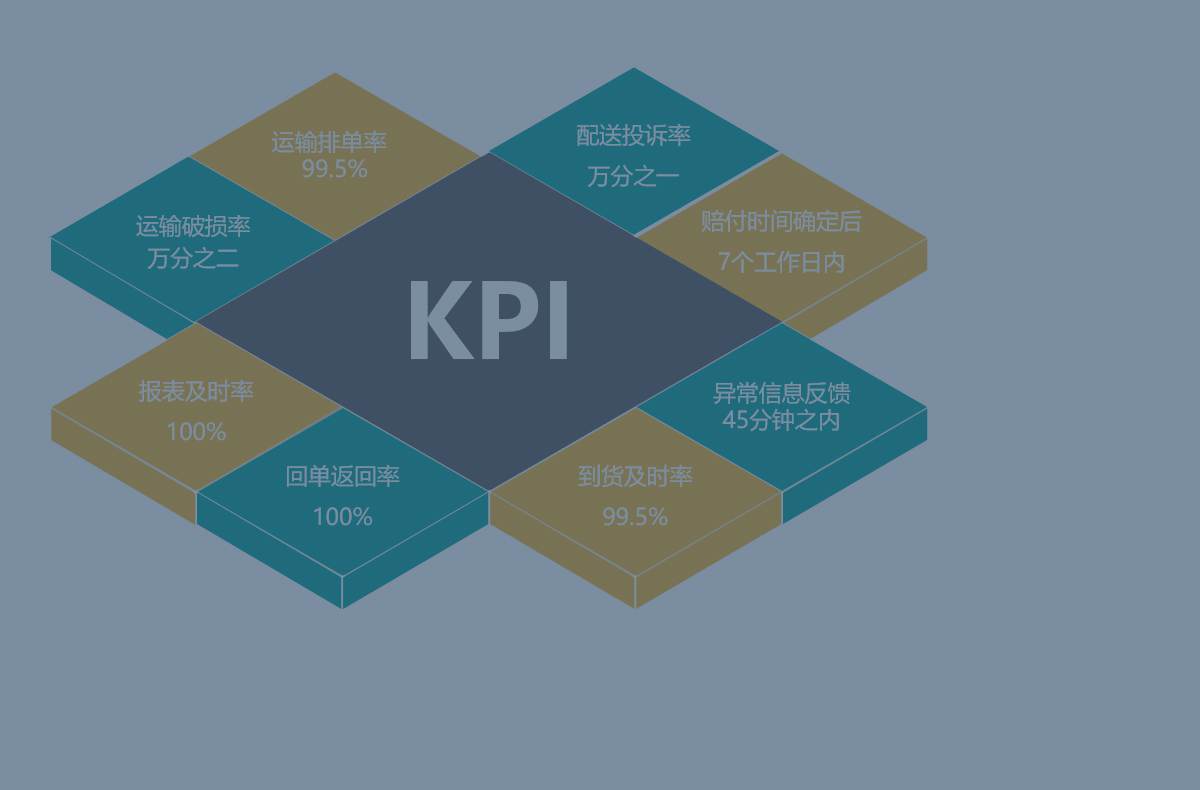
提供1V1售后服务,专业化的客服团队,及时反馈、敏捷响应、专业服务、高效管理端到端的物流供应链,
仓储,产品质检,二次包装,退货处理-按需选择仓储面积与云仓增值服务,满足不同客户的仓储代发货需求!

雨润集团旗下的食品工业企业是中国最大的肉制品生产企业之一。雨润集团下属200多家···

茶百道,成立于2008年,是正在创造惊喜生活的新式茶饮品牌,希望通过产品开发和潮···
迈大食品(山东)有限公司由迈大集团(MAYORA集团)投资,迈大集团成立于197···

世界上每三个面包中有一个就是用乐斯福酵母制作而成。乐斯福作为来自法国北部、具有1···
平文冷链物流与茶百道达成合作:···【详情+】

平文家人们!春暖花开,春意盎然···【详情+】

什么是云仓代发货顾名思义,其实···【详情+】


智慧冷链仓库配备了各种系统,以提高效率、···【详情+】